本帖最后由 kay2kay 于 2021-03-14 18:10 编辑
本文为本人的滴水逆向破解脱壳学习笔记之一,为本人对以往所学的回顾和总结,可能会有谬误之处,欢迎大家指出。
陆续将不断有笔记放出,希望能对想要入门的萌新有所帮助,一起进步
所有笔记链接:
大神论坛 逆向脱壳分析基础学习笔记一 进制篇
大神论坛 逆向脱壳分析基础学习笔记二 数据宽度和逻辑运算
大神论坛 逆向脱壳分析基础学习笔记三 通用寄存器和内存读写
大神论坛 逆向脱壳分析基础学习笔记四 堆栈篇
大神论坛 逆向脱壳分析基础学习笔记五 标志寄存器
大神论坛 逆向脱壳分析基础学习笔记六 汇编跳转和比较指令
大神论坛 逆向脱壳分析基础学习笔记七 堆栈图(重点)(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记八 反汇编分析C语言
大神论坛 逆向脱壳分析基础学习笔记九 C语言内联汇编和调用协定
大神论坛 逆向脱壳分析基础学习笔记十 汇编寻找C程序入口(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记十一 汇编C语言基本类型
大神论坛 逆向脱壳分析基础学习笔记十二 汇编 全局和局部 变量(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记十三 汇编C语言类型转换(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记十四 汇编嵌套if else(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记十五 汇编比较三种循环(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记十六 汇编一维数组(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记十七 汇编二维数组 位移 乘法(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记十八 汇编 结构体和内存对齐(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记十九 汇编switch比较if else(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记二十 汇编 指针(一)(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记二十一 汇编 指针(二)(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记二十二 汇编 指针(三)(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记二十三 汇编 指针(四)(需登录才能访问)
大神论坛 逆向脱壳分析基础学习笔记二十四 汇编 指针(五) 系列完结(需登录才能访问) 更多逆向脱壳资源,请访问 大神论坛C语言基本类型不同于寻常的C语言基本数据类型的学习,这里以汇编的形式来学习不同数据类型的存储方式和差异 C语言的数据类型C语言的基本类型属于C语言的数据类型的一部分: 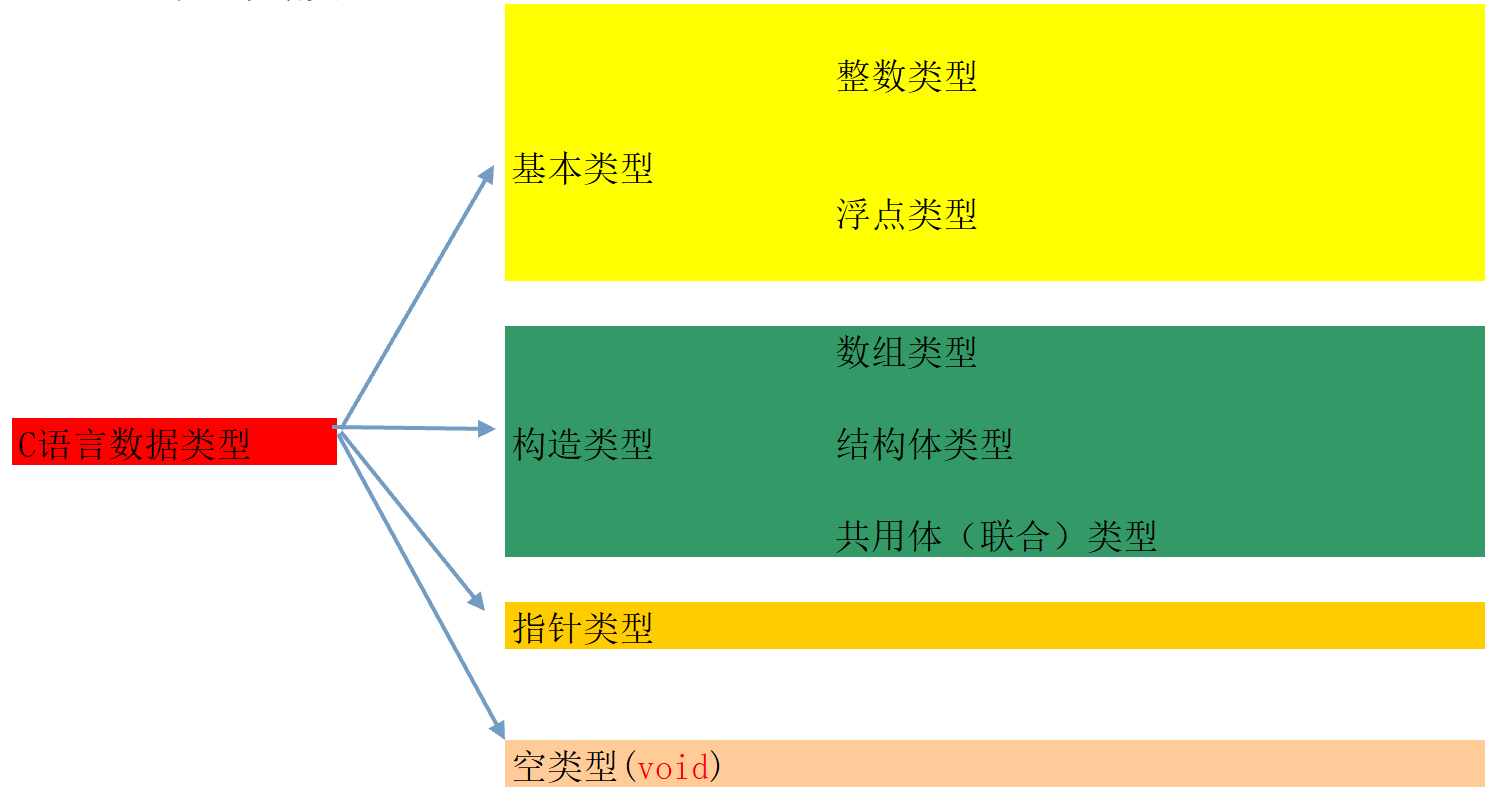
这里先从最简单的基本类型进行入手学习,在学习基本类型之前再温故一下先前学习过的汇编的数据类型 汇编的数据类型| 数据类型 | 名称 | 位 |
|---|
| BYTE | 字节 | 8BIT | | WORD | 字=2字节 | 16BIT | | DWORD | 双字=4字节 | 32BIT |
整数类型C语言的整数类型有:char short int long | 整数类型 | 位 | 字节 | 对应汇编 |
|---|
| char | 8BIT | 1字节 | byte | | short | 16BIT | 2字节 | word | | int | 32BIT | 4字节 | dword | | long | 32BIT | 4字节 | dword |
大家可能会觉得疑惑,为什么int和long所表示的貌似一样? 这其实是历史遗留问题,在以前的16位计算机中,int的长度位2字节,但是在32位计算机中,int类型变成了4字节,而long类型原来便是4字节,现在在仍然是4字节
存储方式接下来从汇编的角度来看看整数类型如何存储 #include "stdafx.h"
int main(int argc, char* argv[])
{
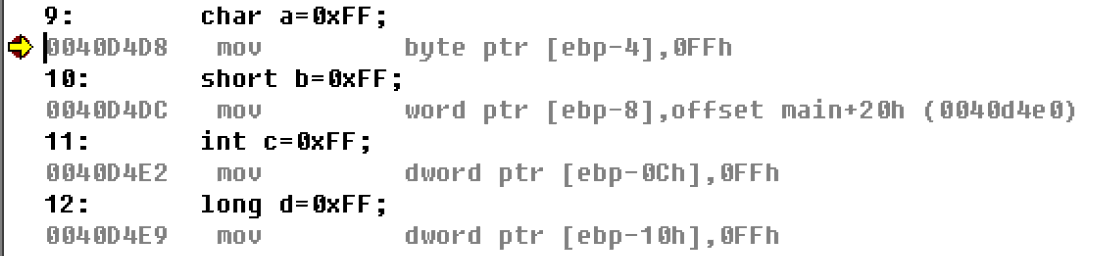
char a=0xFF;
short b=0xFF;
int c=0xFF;
long d=0xFF;
return 0;
}
| 语句 | 对应汇编 | 单位 |
|---|
| char a=0xFF; | mov byte ptr [ebp-4],0FFh | byte | | short b=0xFF; | mov word ptr [ebp-8],offset main+20h (0040d4e0) | word | | int c=0xFF; | mov dword ptr [ebp-0Ch],0FFh | dword | | long d=0xFF; | mov dword ptr [ebp-10h],0FFh | dword |
超出数据宽度赋值上面的赋值都是在基本类型的数据宽度之内,那么如果超出数据宽度会如何? 修改赋值的内容为0x123456789 #include "stdafx.h"
int main(int argc, char* argv[])
{
char a=0x123456789;
short b=0x123456789;
int c=0x123456789;
long d=0x123456789;
return 0;
}
然后再观察反汇编代码 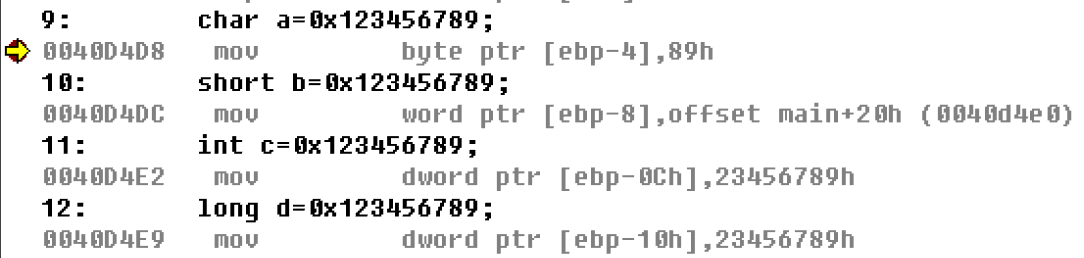
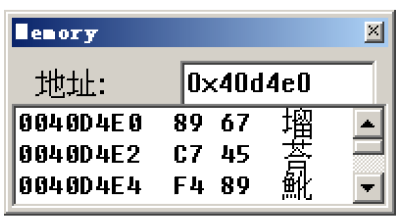
| 语句 | 对应汇编 | 实际赋值 | 单位 |
|---|
| char a=0x123456789; | mov byte ptr [ebp-4],89h | 89h | byte | | short b=0x123456789; | mov word ptr [ebp-8],offset main+20h (0040d4e0) | 6789h | word | | int c=0x123456789; | mov dword ptr [ebp-0Ch],23456789h | 23456789h | dword | | long d=0x123456789; | mov dword ptr [ebp-10h],23456789h | 23456789h | dword |
不难发现,所有赋值语句全部都高位截断了,即高位的部分全部舍去,只赋值了数据的低位 有符号数和无符号数分析整数类型分为有符号(signed)和无符号(unsigned)两种 默认就是有符号的类型 通过汇编观察有符号和无符号在内存中存储时是否有差别,这里以char 为例 #include "stdafx.h"
int main(int argc, char* argv[])
{
char signed a=0xFF;
char unsigned b=0xFF;
return 0;
}

我们发现无符号数和有符号数在内存存储中并无差别,再一次印证了我们前面所学的:计算机并不关心数据是有符号数还是无符号数,决定一个数据是有符号数还是无符号数的是使用数据的我们,同一个数据使用不同的方式来解析 了解了有符号数和无符号数的本质后,再来谈谈有符号数和无符号数的注意事项 有符号数和无符号数注意场景比较大小同为有符号数时#include "stdafx.h"
int main(int argc, char* argv[])
{
char a=0xFF;
char b=1;
if(a>b){
printf("a>b\n");
}else if(a<b){
printf("a<b\n");
}else{
printf("a=b\n");
}
return 0;
}
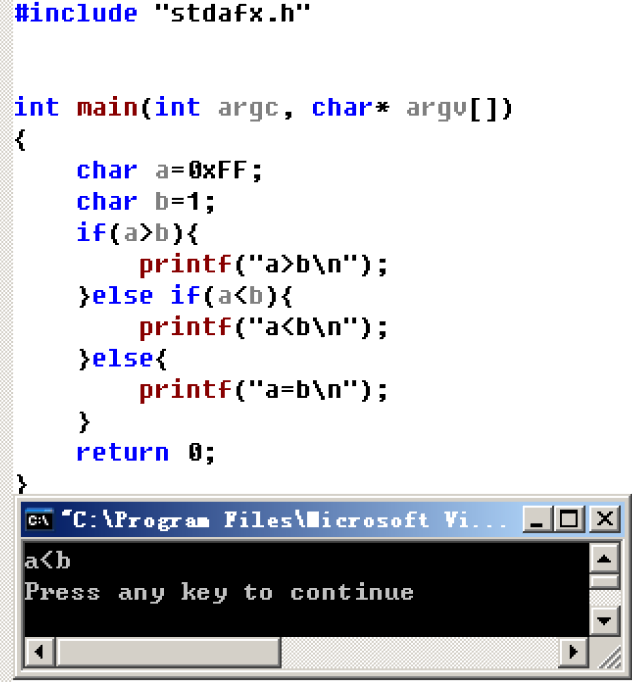
同为无符号数时#include "stdafx.h"
int main(int argc, char* argv[])
{
char unsigned a=0xFF;
char unsigned b=1;
if(a>b){
printf("a>b\n");
}else if(a<b){
printf("a<b\n");
}else{
printf("a=b\n");
}
return 0;
}
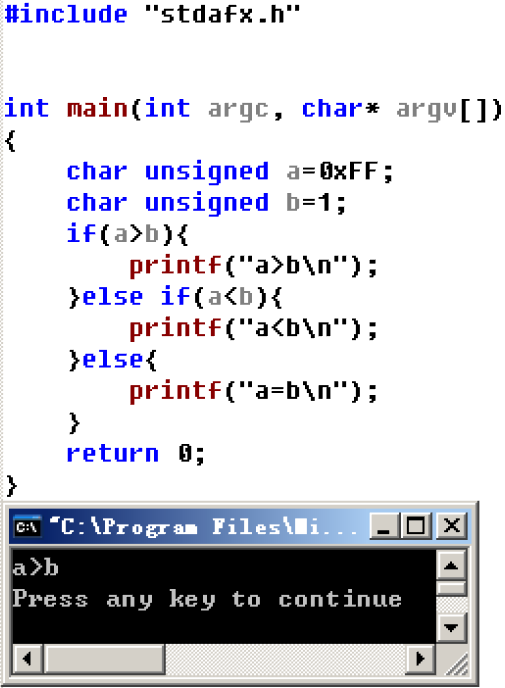
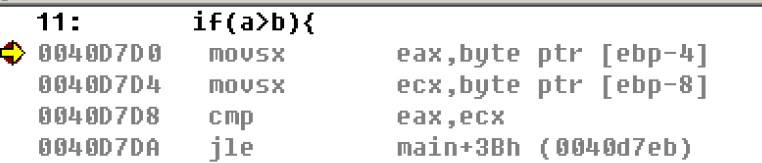
汇编比较大小看到这里,可能就会产生疑问,既然在内存中数据的存储是一样的,那么如何进行比较呢? 这里就要梦回先前的汇编跳转和比较指令 char的比较我们可以看到: 比较有符号数char a=0xFF;
char b=1;
if(a>b){
printf("a>b\n");
}
比较无符号数char unsigned a=0xFF;
char unsigned b=1;
if(a>b){
printf("a>b\n");
}
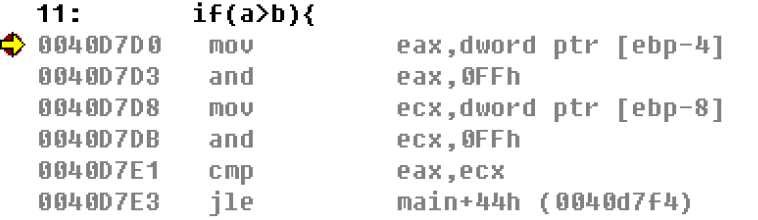
我们发现这里的使用的jcc语句都是jle:jump less equal 小于等于才跳转(有符号数),和我们的a>b正好相反 但是我们会发现在有符号数那里使用了movsx指令,该指令为汇编语言数据传送指令MOV的变体。带符号扩展,并传送。 即它会将char从原本的byte扩展到dword,这样一来数据长度被扩展以后,自然就可以使用同一个jle指令来进行比较 int的比较前面char的比较是通过数据宽度的扩展来实现比较的,那么当使用int时,无法扩展符号的数据宽度时,如何比较? 将上面的char改为int后再次观察反汇编代码 比较有符号数int a=0xFF;
int b=1;
if(a>b){
printf("a>b\n");
}

比较无符号数int unsigned a=0xFF;
int unsigned b=1;
if(a>b){
printf("a>b\n");
}

差别我们可以发现,同样是比较,比较无符号数和有符号数时,分别对应两个不同的jcc语句 | 比较 | jcc语句 | 含义 |
|---|
| 比较有符号数 | jle main+3Dh(0040d7ed) | 小于等于则跳转 (有符号数) | | 比较无符号数 | jbe main+3Dh(0040d7ed) | 小于等于则跳转 (无符号数) |
浮点类型C语言的浮点类型分为float和double 存储方式和规范float和double在存储方式上都是遵从IEEE规范的 float的存储方式如下图所示: 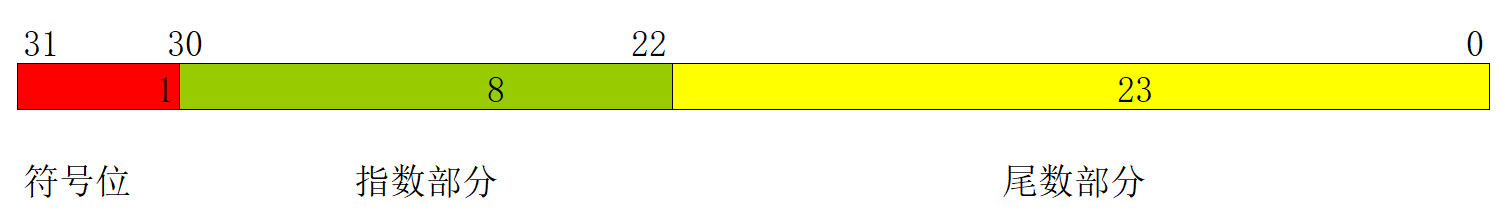
double的存储方式如下图所示: 
由于double的长度比较长,我们下面就用float作为例子,实际上,double不过是比float精度更高了,在将浮点数转化为存储到内存中的二进制的步骤几乎一致 转化步骤将一个float型转化为内存存储格式的步骤为: - 先将这个实数的绝对值化为二进制格式
- 将这个二进制格式实数的小数点左移或右移n位,直到小数点移动到第一个有效数字的右边
- 从小数点右边第一位开始数出二十三位数字放入第22到第0位。
- 如果实数是正的,则在第31位放入“0”,否则放入“1”
- 如果n是左移得到的,说明指数是正的,第30位放入“1”。如果n是右移得到的或n=0,则第30位放入“0”
- 如果n是左移得到的,则将n减去1后化为二进制,并在左边加“0”补足七位,放入第29到第23位。 如果n是右移得到的或n=0,则将n化为二进制后在左边加“0”补足七位,再各位求反,再放入第29到第23位
看起来很复杂QAQ,但结合下面的实例来看就还好(。・∀・)ノ゙ 在转化步骤中的第一步,又分为整数部分的二进制化和小数部分的二进制化 十进制整数二进制化采用除留余数法 比如将11转化成二进制数 | 计算 | 余数 |
|---|
| 11/2=5 | 1 | | 5/2=2 | 1 | | 2/2=1 | 0 | | 1/2=0 | 1 | | 0 | 结束 |
11二进制表示为(从下往上):1011 注意到只要除以后结果为0便结束了,任意整数不断除以2最终都会等于0,因此所有整数都可以用二进制来精确表示 十进制小数二进制化采用乘二取整法 比如将0.9转化为二进制数 | 计算 | 取整数部分 |
|---|
| 0.9*2=1.8 | 1 | | 0.8(前面结果的小数部分)*2=1.6 | 1 | | 0.6*2=1.2 | 1 | | 0.2*2=0.4 | 0 | | 0.4*2=0.8 | 0 | | 0.8*2=1.6 | 1 | | 0.6*2=1.2 | 1 | | …… | …… |
0.9二进制表示为(从上往下):110011…… 很显然,上面的计算过程循环了,也就是说*2永远不可能消灭小数部分,这样算法将无限下去。很显然,并非所有的小数都可以用二进制精确表示,就和十进制里也无法精确表示出1/3一样 实例8.25f#include "stdafx.h"
int main(int argc, char* argv[])
{
float i=8.25f;
return 0;
}
我们用反汇编查看8.25f 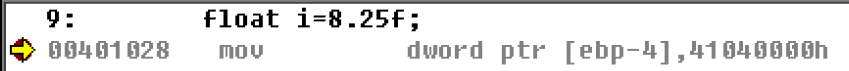
00401028 mov dword ptr [ebp-4],41040000h
我们会发现8.25f的表现形式为41040000h,接下来我们就来研究这个41040000h是怎么来的 一步步按先前提到的转化步骤来: 实数的绝对值化为二进制格式先处理整数部分8.25 | 计算 | 余数 |
|---|
| 8/2=4 | 0 | | 4/2=2 | 0 | | 2/2=1 | 0 | | 1/2=0 | 1 |
整数部分8转化为二进制:1000(从下往上) 再处理小数部分8.25 | 计算 | 取整数部分 |
|---|
| 0.25*2=0.5 | 0 | | 0.5*2=1.0 | 1 |
0.25转化为二进制可表示为:01(从上往下) 于是8.25用二进制可表示为1000.01 填充尾数接下来先填充尾数部分 先将二进制数转为用科学计数法表示 1000.01=1.00001*2的3次方 (小数点向左移动3位 指数为3) 1.**00001***2 就是将小数点后面的23位填入尾数部分,我们这里小数部分恰好能够精确地转化为二进制数,于是剩下的部分用0填充即可 如果是前面的0.9转化为的0.110011……=1.1100……*2的-1次方 则是截取小数点后面的23位填入1100…… | 符号位 | 指数部分 | 尾数部分 |
|---|
| 占用空间 | 1 | 8 | 23 | | 存储内容 | | | 00001000000000000000000 |
此时尾部部分已经填充完毕,再填充符号位 填充符号位符号位就简单多了,正数填充0,负数填充1即可 这里我们的8.5f是正数,填0结束 | 符号位 | 指数部分 | 尾数部分 |
|---|
| 占用空间 | 1 | 8 | 23 | | 存储内容 | 0 | | 00001000000000000000000 |
填充指数部分指数部分的最高位填充看前面是前面将二进制数科学计数法化时,是进行了左移还是右移,左移填1,右移填0 前面我们得到了8.5f的转化: 1000.01=1.00001*2的3次方 (小数点向左移动3位 指数为3) 很明显我们的是左移,因此,最高位填写1 剩下的部分则是用指数减去1后二进制化填充即可 8.5f的指数为3,3-1=2 2的二进制为10 所以指数部分应该为: 10000010 于是整个填充完成 | 符号位 | 指数部分 | 尾数部分 |
|---|
| 占用空间 | 1 | 8 | 23 | | 存储内容 | 0 | 10000010 | 00001000000000000000000 |
总共为0100 0001 0000 0100 0000 0000 0000 0000 转化为十六进制为4 1 0 4 0 0 0 0 0 和我们前面用汇编看到的结果一致 -8.25f#include "stdafx.h"
int main(int argc, char* argv[])
{
float i=-8.25f;
return 0;
}
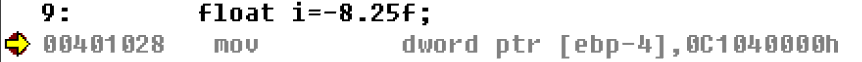
00401028 mov dword ptr [ebp-4],0C1040000h
-8.25f和8.25f相差的只有符号位,于是将前面的8.25f的符号位改为1即可 | 符号位 | 指数部分 | 尾数部分 |
|---|
| 占用空间 | 1 | 8 | 23 | | 存储内容 | 1 | 10000010 | 00001000000000000000000 |
也就是1100 0001 0000 0100 0000 0000 0000 0000 转为十六进制是 C 1 0 4 0 0 0 0 和前面反汇编看到的结果一致 0.25f这次看个纯小数在内存中如何存储,依旧采取相同的套路 实数的绝对值化为二进制格式| 计算 | 取整数部分 |
|---|
| 0.25*2=0.5 | 0 | | 0.5*1=1.0 | 1 |
0.25f转化为二进制:0.01 填充尾数科学计数法表示:0.01=1.0*2的-2次方 (小数点向右移动2位 指数为-2 ) 尾数填充0,1.0小数点后面全为0,于是尾数全部填0即可 | 符号位 | 指数部分 | 尾数部分 |
|---|
| 占用空间 | 1 | 8 | 23 | | 存储内容 | | | 00000000000000000000000 |
填充符号位0.25f是正数直接填充0即可 | 符号位 | 指数部分 | 尾数部分 |
|---|
| 占用空间 | 1 | 8 | 23 | | 存储内容 | 0 | | 00000000000000000000000 |
填充指数部分科学计数法表示:0.01=1.0*2的-2次方 (小数点向右移动2位 指数为-2 ) 向右移动,指数部分最高位填0 指数为-2,-2-1=-3 将-3转化为二进制:-3的十六进制对应fd,fd转为二进制:1111 1101 不知道为什么-3对应fd的可以看这里:逆向基础笔记二 数据宽度和逻辑运算 我们发现-3转为二进制共有8位,但是指数部分总共也只有8位,其中最高位还用作表示是右移填充了0,于是只截取低7位填充进指数部分剩下的内容 于是整个填充完成 | 符号位 | 指数部分 | 尾数部分 |
|---|
| 占用空间 | 1 | 8 | 23 | | 存储内容 | 0 | 01111101 | 00000000000000000000000 |
总共为0011 1110 1000 0000 0000 0000 0000 0000 转化为十六进制为3 e 8 0 0 0 0 0 接下来用反汇编验证一下: 
得到的结果是一致的,好耶ヽ(✿゚▽゚)ノ
|
 发表于 2021-03-14 18:10
发表于 2021-03-14 18:10